The Most Mind-Blowing Thing I Know of in Physics
About a year or two ago, I stumbled across an interesting question asked by a user named 32koala on Reddit’s AskScience board: “Is light made of particles, or waves?” With my quantum physics course still in recent memory, and having thoroughly enjoyed Eliezer Yudkowsky’s excellent quantum physics sequence (on which this post is heavily based), I found that the answers the commenters had given didn’t quite elaborate or clarify things enough for my liking. I asked people if they wanted a more thorough explanation, and after receiving several comments from people expressing their interest, I gave it to them. In my perennial tradition of not wanting to half-ass things, it ended up being even longer than I expected and I spent a lot of time afterwards answering questions to the best of my ability at the time. It got a reasonable amount of attention for the day, and I got comments saying that it deserved a better home than a comment buried in the depths of a Reddit thread.
It took over a year, but I’ve finally followed through that suggestion. I’ve cleaned it up slightly from its initial version, but for the most part the content is similar to the original Reddit comment.
What is light, anyway?
Let’s start with the initial question — light, is it a particle, or a wave? As it turns out, light exhibits properties of both. Let’s take these two ways of seeing light individually. I’m going to take this painfully slowly, so feel free to skip some of this stuff if you already know it.
Light as a wave
I’m hoping everyone here knows what interference is. If you don’t, take a look at the image below:
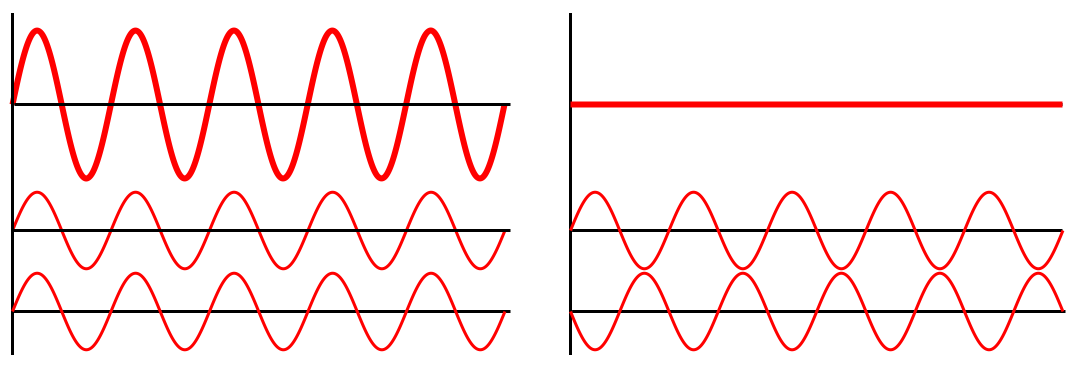
Interference of two waves — Image source
On either side, you have two smaller waves at the bottom, and the one on the top is what you get when you add them up. Depending on how “in-sync” the two waves are (their phase), you could end up with a wave that’s twice as big (“constructive interference”), or the two waves could cancel each other out (“destructive interference”), or you could get anything in between. It turns out that light behaves in exactly this way, and the classic example of this is the double-slit experiment.
If you shine light at a small slit, it makes a nice round wave that looks a lot like ripples in a pond. This is due to a phenomenon called diffraction, which is found in things like water as well — if you have a flat wave coming at an obstacle with a slit in it, the wave “bends” around the corners of the obstacle and creates something that’s roughly circular, if your slit is small enough, as in the image below:
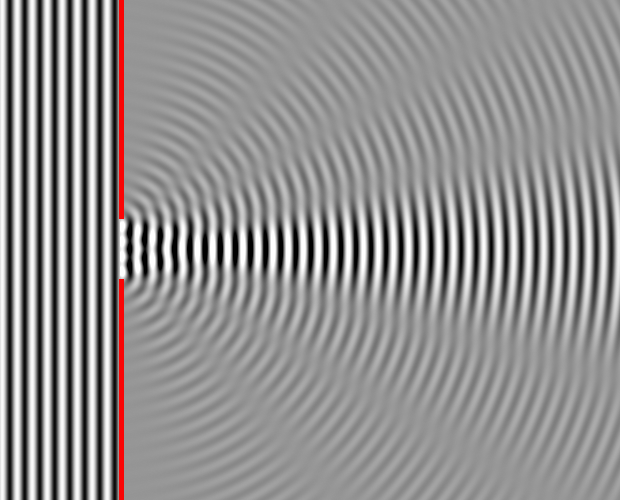
Diffraction of a wave — Image source
Light does this as well. If you shine a light at a small enough slit, you end up with a spread-out sort of pattern caused by the light beam “bending” around the corners of the slit.

Light diffracting through a slit — Image source
But what happens if you get two of these slits, and put them close enough together? Then the waves start interfering. Because of the way these waves are oriented, you get parts of the new wave that interfere constructively, giving you twice the brightness, and parts that interfere destructively, giving complete darkness, and you end up with a nice little pattern of bands. All this makes sense if you think of light as a wave.
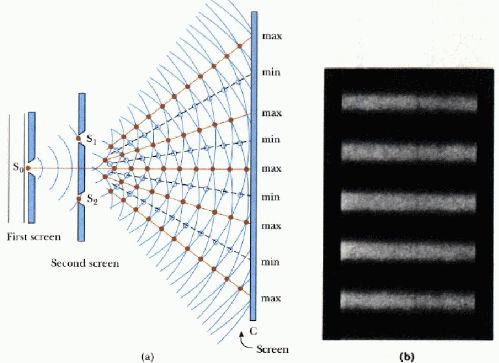
The double-slit experiment — Image source
Let’s step aside for a moment and talk a bit about what happens to a light wave as it reflects off a mirror. Roughly speaking, whenever light is reflected off a mirror at a right angle, it gets its phase changed by 90°. In other words, look at the red line in the graph below — notice the wave’s repeating pattern? It gets shifted backwards by about one quarter of the length of that repeating pattern, forming the blue line.
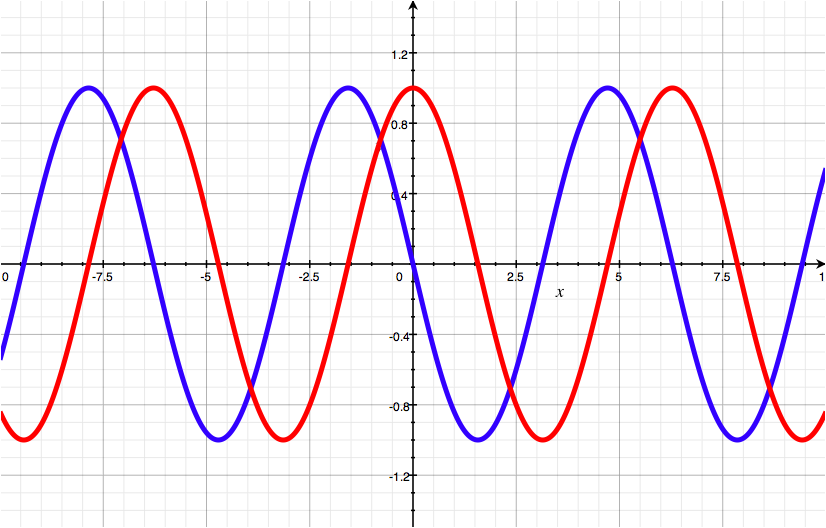
The red line is shifted backwards by a quarter of its wavelength, forming the blue line — Alternate, interactive version here
This lets us do some cool things with mirrors to study interference. There’s one type of mirror that’s pretty useful for these kinds of experiments, and that’s the half-silvered mirror — a neat little mirror that reflects only half the light shone onto it, and lets the other half pass through.
Take a look at this experiment here:
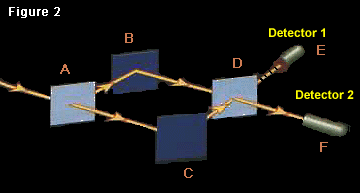
The half-silvered mirror experiment — Image source
In this configuration, A and D are half-silvered mirrors, while B and C are normal ones. Mirror A splits the beam of light into two, and at mirror D each of the two beams is split again, and goes into both detectors. If you study this closely, you’ll find that there are four paths the light can go through: ABDE, ABDF, ACDE, and ACDF. Furthermore, at the end of the experiment, beams ABDE and ACDE end up joining together and going to the same place, as do beams ABDF and ACDF. Let’s look at these two pairs.
Both ABDF and ACDF are reflected exactly twice, which means they get phase shifted by 90°+90° = 180°. But since they both get shifted by the same amount, they stay “in-sync” (in phase), and therefore interfere constructively.
ABDE and ACDE are a different matter. ABDE gets reflected three times (a 270° shift), while ABDE only gets reflected once (a 90° shift). This means that the difference in their phases ends up being 270° - 90° = 180°, meaning they are completely “out of sync” (out of phase), and interfere destructively.
What this all ends up boiling down to is that you get all of the light flowing towards F, and none of it flowing towards E. And again, this all makes perfect sense when you think of light as a wave.
Light as a particle
As it turns out, though, light has some behaviour that is inconsistent with the idea of it as a continuous wave like ripples in a pond. (Fun side-note: before the discoveries that led to the concepts of the photon and relativity, this is exactly what scientists thought light was — some kind of ripple in a mysterious “aether”.) It was discovered that light gave its energy in fixed amounts — its amounts being equivalent to the light’s frequency (how fast the wave is waving) multiplied by a number now known as Planck’s constant (usually denoted as h, and whose value is 6.62×10−34 Js).
This is a rather baffling result if you consider light a wave — it’s like having a pond in your backyard where the ripples can be 1 cm high or 2 cm high, but can’t be any other height in between. So the concept of the photon came about, that light was a series of point-like particles flying around in space. Further experiments supported this model.
(Fun fact #2: This is where the term quantum comes from — the energy in photons and other particles is said to be quantized)
Where it all breaks down
All this presented a problem, though, because now, somehow, the two seemingly very different models of light had to somehow be reconciled. And it gets weirder from there.
Remember those interference experiments we talked about earlier? Turns out the interference still happens even if only one photon is sent through at a time. Consider the double-slit experiment. Those bright areas that you saw? As it turns out, a photon is more likely to end up hitting one of those areas than the darker areas. You can see that pretty clearly in the animation below (though this was done with electrons, the concept is the same) — each dot is where a particle hit, and you can clearly see the bands of high probability.

An animation of the double-slit experiment done one particle at a time — Image source
The same thing happens with the half-silvered mirror experiment — even if you send one photon at a time, they will always go to only the one detector with 100% probability, never the other.
So, it looks we’re dealing with a wave of probability, then, as strange as that sounds. But it gets stranger.
Let’s take the half-silvered mirror experiment again, but let’s put a sensor in one of the beams that detects the light going by without blocking it, to see if we can tell which path the photon takes.
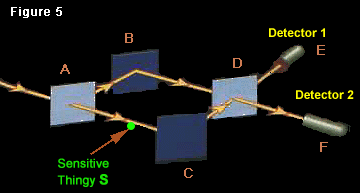
The half-silvered mirror experiment, with a sensor in it this time — Image source
What happens? The interference completely vanishes, and you get an equal chance of the photon going to either detector again. The same thing happens if you try and put a sensor on one of the slits of the double-slit experiment, to see which slit it passes through — poof, interference gone. And everyone is thoroughly baffled.
This is where you have to really plunge into the quantum world to understand it.
Superposition
The best way to think about these things, really, is not to think of them as ripples in a pond nor billiard balls flying around in space, but instead as a flow of probability. In the half-silvered mirror experiment (without the sensor), don’t think of it as “the photon has a 50% chance of being reflected or not reflected”. Instead, realize that the photon takes both paths. 50% of the probability flow is reflected and takes the upper path, while 50% of it is transmitted and follows the lower one. This is what we call a superposition of states — one state is the photon being reflected, the other is it being transmitted through the mirror, and the photon exists in a superposition of these two states, that is, both simultaneously. When these flows join at mirror D, again they take both the path where they’re reflected and the path where they’re transmitted, and because these probability flows are waves that obey the same principles we talked about earlier, the probability flow going into E gets destructively interfered (meaning 0% probability) while the probability flow going into detector F gets constructively interfered (meaning 100% probability).
The same happens in the double-slit experiment — the photon takes every path through the two slits, and the probability waveform interferes with itself to give us that cool band effect.
(A note to any scientists reading this: I’m trying to avoid the whole “squared-modulus” thing here because I’m trying to avoid math as much as possible. To those who are interested, you can refer to other sources. To everyone else, suffice it to say that the math for figuring out the probabilities is slightly more complex than I’m laying it out here.)
Scientific divisions
This still doesn’t really explain why we only see the photon in one place, though, rather than spread out. And unfortunately, this is where modern-day scientists are divided. In general, it seems that whenever we observe or measure a photon, it causes that probability waveform to “collapse” and the photon to show up in only one place. There are two major interpretations of this: one is the Copenhagen Interpretation, and the other is the Many-Worlds Interpretation.
As an important side-note here, though you may have figured it out earlier, these quantum effects don’t just apply to photons — all particles experience these effects, though the bigger they are, the harder it is to see them. (Though interference has already been shown even in large molecules like Buckyballs). In any case, I’m now going to stop talking specifically about photons and start talking about particles in general.
In all honesty, I personally don’t prefer the Copenhagen Interpretation. It’s never made much sense to me. But I’m going to try and explain it as best as I can. The idea behind it is more-or-less what I said in the first paragraph of this section — whenever we try to observe a probability waveform, the wave “collapses”, getting rid of every point of probability except the one where we actually end up seeing the particle. So when you put a detector on your double-slit, it ends up collapsing the photon before its probability wave can create the interference pattern, and the pattern vanishes.
For practical purposes, this works, but I’ve always found it a bit odd, because it never explains why the waveform collapses like this. This is why I prefer the Many-Worlds Interpretation, which I’m going to get into soon. But first, I need to introduce some more concepts.
Decoherence
Let’s consider a particle that’s travelling along in space, and another that’s stationary. Let’s call the travelling one P1 and the stationary one P2. Let’s say that P1 is in a superposition of two states that are in two different positions, one that will collide with P2 (blue), and another that will miss it entirely (red).
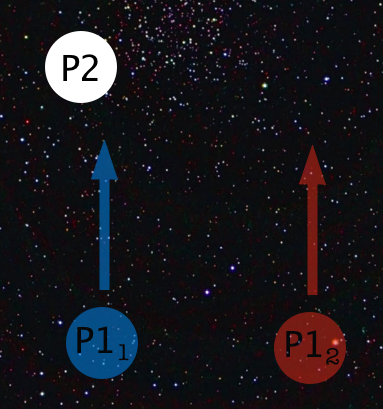
What do you think will happen when P1 reaches P2’s position? Obviously, if it were entirely on the left, they would collide and both go off in different directions, while if it were entirely on the right, P1 would miss P2 completely and continue travelling while P2 stayed in the same place.
But P1 is doing both those things. Both the collision and the non-collision will occur, and you’ll end up with P2 both being collided with and not collided with, flying off and staying perfectly still.
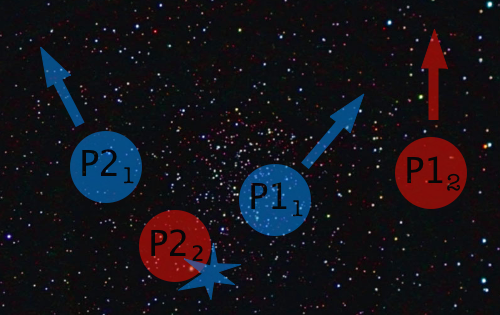
And these two superimposed states are vastly different, meaning that the “blue” state of our little two-particle system is now even more significantly different its “red” state. You can intuit, then, that seeing any sort of interference between P1’s “blue” and “red” states would be much more difficult after it collides with P2. This is a rough explanation of decoherence, where quantum particles have less and less interference as they interact with other particles.
The Real Mind-Blowing Stuff
Okay, so we’ve covered decoherence, but how does this help us understand why we only see the photons in our double-slit experiment in one place? Well, consider this: the screen we’re projecting our photons on to in the experiment, what is it made of?
Atoms. Quantum particles/probability waves.
It makes sense, then, that as the photons pelt the screen, that the atoms in the screen would decohere in the same way that P2 was decohered after P1 (half-)smacked into it. Let me repeat that for emphasis: the whole screen is decohered, is brought into a superposition of states, every time a photon pelts it.
And your eyes that are looking at that screen, receiving photons that are reflecting off it, what are they made of?
The same thing — atoms, particles.
As the photon, superimposed into a billion different states, each of them travelling in a slightly different trajectory, hits the screen, so too does the screen decohere into billions of different states, each one where the photon hit in a slightly different position. And as you stare at that screen, the light bouncing off the screen also decoheres your eyes into a billion different states.
And what about your brain? What is it made of?
As your eyes are decohered into a billion different states, so too are the signals that your eyes send to your brain decohered into a billion different states. And then, as those signals reach your brain, so too is it decohered.
And somewhere within the mess of all these superpositions, one of the superimposed states of you says to your lab assistant, “The photon hit the left side of the screen,” while simultaneously another one of the superimposed states of you says “The photon hit the right side of the screen”. And both of these would be equally real, as real as what you’re experiencing right now.
That, my friends, is the Many-Worlds interpretation of quantum physics — that your body, brain, and everything around you is constantly being decohered into a superposition of very different states by every single photon, every single particle, that interacts with it.
And that is the most mind-blowing thing I know of in physics.